ECLISSI

Le eclissi di Sole e di Luna (che per lungo tempo furono causa di terrore per l’umanità; un esempio per tutti: la battaglia fra Medi e Lidi nel VI secolo a.c. fu interrotta da un’eclisse di Sole che terrorizzò i guerrieri!) avvengono per interposizione della Luna tra il Sole e la Terra (eclisse di Sole) che nasconde, eclissa, tutto o in parte il disco solare; o all’interposizione della Terra tra il Sole e la Luna (eclissi di Luna); la Terra intercetta parzialmente o totalmente i raggi che dal Sole andrebbero alla Luna. Si rammenta che la Luna non ha atmosfera. Ricordando che il piano dell’orbita della Luna è inclinato di 5°9′ rispetto all’eclittica, affinché si verifichi un’eclisse di Sole occorre che siano soddisfatte due condizioni:

1) Luna al novilunio, 2) luna in prossimità dell’ eclittica, cioè luna vicina ad uno dei suoi due nodi: la Terra può così intercettare il cono d’ombra della Luna (fig. 1).

Affinché si verifichi un’eclissi di Luna occorre:

1) Luna al plenilunio, 2) luna in prossimità di uno dei suoi nodi: può così entrare nel cono d’ombra della Terra.

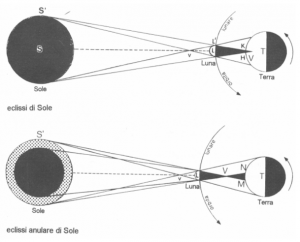
Eclisse di Sole

Dopo aver condotto le rette tangenti ai dischi del Sole e della Luna si formano i coni d’ombra aventi i vertici in Ve i coni di penombra aventi i vertici in v; le distanze dei vertici della Luna dipendono dalle reciproche posizioni Sole-Luna.

Si hanno i seguenti casi:

Fig. 1

eclisse totale: il vertice V è dentro o al di là della T erra ad una distanza dal centro della Luna che può raggiungere 59,7 R (quando il Sole è all’apogeo e la Luna al perigeo). La zona KH della superficie terrestre intercetta il cono d’ombra. Gli osservatori della zona, mobile, HK non vedono il sole che è occultato dalla luna.

eclisse centrale: è la fase centrale dell’ eclissi totale; l’osservatore al centro della zona KH è nel piano passante per i centri degli astri.

eclisse anulare: il vertice V non raggiunge la Terra ed è ad una distanza dal centro della Luna che può scendere fino a 57,7 R (quando il sole è al perigeo e la luna all’apogeo). La zona NM della superficie terrestre intercetta il cono opposto del cono d’ombra.

Gli osservatori della zona, mobile, MN vedono una sottile corona circolare della fotosfera non riuscendo, il disco della luna, a coprire l’intero disco del sole.

eclisse parziale: è osservato dagli osservatori che si trovano fuori del cono d’ombra, ma comunque nel cono di penombra di vertice V; a seconda del luogo potrà essere seguito o preceduto dall’eclisse totale- anulare.

Si ricorda, in merito all’ eclissi totale, che la distanza perigea della luna è circa 56 R e che il diametro della Luna è 33′.8 mentre quello medio del Sole è 32′. In merito all’ eclissi anulare si fa presente che la distanza apogea della luna è 63,8 R ed il suo diametro apparente è 29′.3. Alla distanza media Terra-Sole di 23400 R il diametro apparente del sole è 32′.

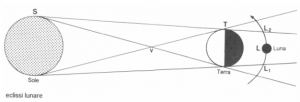
Eclisse di Luna

Nella fase di plenilunio in vicinanza dell’eclittica la luna si immerge nel cono d’ombra della Terra. Il vertice V dista dal centro della Terra della distanza TV = 216R, valore medio; la distanza Terra-Luna è, in media, 60R. La sezione normale del cono d’ombra, in pratica la distanza tra LI e 0. (fig. 2) è uguale a 0,73R; la luna ha un raggio di circa 0,27 R e pertanto s’immerge totalmente nel cono d’ombra. L’arco (L 1 L 2 ) è ampio 83′.2; il disco lunare ha un diametro apparente di 31′.2.

Per calcolare la durata di un eclisse centrale si esegue il rapporto (83′.2 – 31′.2) : 30′.6 dove 30′.6 è la velocità oraria della rivoluzione sinodica. Il valore del rapporto è l h 42 m circa. La durata di un’eclisse centrale, dal contatto del bordo di levante fino al contatto del bordo di ponente, è 2 h 43 m (83′.2 : 30′.6). Se, come accade in generale, la traiettoria relativa della Luna, rispetto al cono d’ombra, non passa per l’asse, il tempo dell’eclisse si riduce; può anche aversi, come facilmente si può immaginare, un’ eclissi parziale di Luna quando non tutto il satellite entra nel cono d’ombra della T erra. L’eclissi di luna è osservabile da tutti i luoghi della T erra che hanno la luna sopra l’orizzonte, cioè da poco più di mezza superficie terrestre, tenendo conto della rotazione terrestre durante l’eclissi. Avvenendo il fenomeno in plenilunio esso è osservabile durante le ore notturne.

Fig. 2

Non si ha un completo oscuramento del disco lunare; la parte immersa nel cono d’ombra assume colore rosso bruno. Ciò è dovuto al fatto che i raggi solari, nell’attraversare l’atmosfera terrestre,Eclissi e Librazioni della luna 3 subiscono una rifrazione che li fa incurvare con la convessità verso il suolo. Conseguentemente si ha un cono d’ombra ottico completamente buio che ha il vertice a soli 42R. La luna, essendo a 60R, riceve i raggi solari meno rifratti, cioè quelli rossi, donde il colore rosso bruno assunto dal disco lunare durante l’eclissi. Minore importanza e suggestione danno i passaggi della Luna nel cono di penombra, il cui vertice è v; ivi la luna perde parte della sua luminosità.

LIBRAZIONI LUNARI

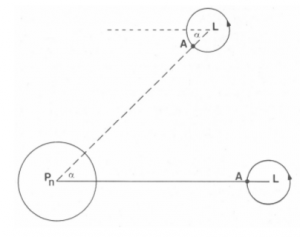
La Luna compie una rotazione intorno al proprio asse nel medesimo tempo che impiega a rivoluzionare intorno alla Terra: 27 d 7 h 43 m 12 s . In figura 3 l’angolo α , in Pn (α n ), di rivoluzione in un determinato intervallo, è uguale all’angolo α (in L) di rotazione. Il punto A della Luna, centro dell’emisfero che il nostro satellite rivolge alla Terra, rimane sempre sulla congiungente dei centri satellite-pianeta. Se le cose stessero proprio in questi termini si dovrebbe concludere che dalla Terra sarebbe visibile sempre e soltanto la stessa metà della superficie lunare. Ma è facile rendersi conto, anche con un modesto cannocchiale, che sono visibili, periodicamente, altre zone del suolo selenico, limitrofe al circolo delimitante l’emisfero visibile; ciò grazie ad oscillazioni o « librazioni » che consentono di vedere 6/10 della superficie lunare. Un’oscillazione è la librazione in longitudine: la Luna ha una velocità orbitale continuamente variabile, in ossequio alla seconda legge di Keplero. Inoltre la velocità di rotazione intorno al proprio asse non è rigorosamente uniforme.

Queste due cause fanno sì che laα Pn sia lievemente differente da α . Da qui le oscillazioni del punto A dal centro del circolo delimitante l’emisfero visibile della Terra. Una seconda causa è la librazione in latitudine: per capirla cominciamo col dire che se L fosse uno dei due poli della Luna, l’asse polare lunare risulterebbe perpendicolare al piano dell’ orbita (piano del foglio della fig. 3) ed il circolo delimitante passerebbe costantemente per i poli; poiché l’asse di rotazione è inclinato, rispetto alla perpendicolare al piano dell’orbita, di un angolo di 6°,5 circa (così come l’asse terrestre è inclinato di 23°27′ rispetto alla perpendicolare al piano dell’ eclittica) conseguentemente si scoprono, del suolo selenico, alternativamente le calotte polari nord e sud. Infine la librazione diurna è dovuta al percorso circolare che ognuno di noi fa nello spazio nel periodo che va dal sorgere al tramonto della Luna. Questo percorso ha un raggio di Km 6371∙ cosq φ e non è trascurabile rispetto alla distanza Terra-Luna. Pertanto, cambiando punto di osservazione, si sposta lievemente il circolo delimitante l’emisfero visibile del satellite.

Fig. 3

Il calendario.

Si fa derivare, questa denominazione, da Calendarium che designava presso i Romani un libro commerciale nel quale si annotavano gli interessi che si maturavano il primo giorno (calende) di ogni mese sui capitali dati a prestito. Come regola pratica di computo del tempo il calendario può avere come unità di misura il giorno, il mese del ciclo delle fasi lunari, l’anno tropico che raggruppa le quattro stagioni. Il calendario si trasforma nei secoli e nei millenni a seconda del grado di civiltà e degli interessi dei vari popoli. Sicché si hanno calendari dei popoli primitivi dell’America (Messicani, Maya, Aztechi); dell’estremo oriente (cinese e giapponese); dell’Asia (indiano, iranico, persiano, armeno); calendari semitici (mesopotamico, ebraico), egiziano, copto, greco e romano antico. Diremo di quest’ultimo cui si lega il nostro attuale calendario, in uso presso quasi tutti i popoli civili.

Sembra che il calendario romuleo avesse per unità fondamentale l’anno di dieci mesi con aggiunta periodica di qualche mese per accordarlo col ciclo stagionale. Fu riformato da Numa Pompilio che adottò, con alcune correzioni, il calendario greco, così che l’anno si compose di 12 mesi della durata complessiva di 355 giorni (dispari, secondo l’uso augurale!) e quindi con l’aggiunta dei mesi di gennaio e febbraio che mancavano nel calendario precedente. Per riportare poi il periodo annuale in accordo col ciclo stagionale (365 giorni e 1/4 circa) s’intercalava dopo il 23 febbraio, in anni alterni, un mese (mercedonio) di giorni variabili nel numero. Decideva, in tal senso, il Consiglio dei Pontefici, peraltro abusando di tale facoltà per motivi diversi da quelli cronologici.

L’anno risultava di 366,5 giorni. Col trascorrere dei secoli l’imperfezione di questo calendario diventò rilevantissima, rispetto alle date astronomiche (una differenza di 90 giorni circa, ai tempi di Giulio Cesare, tra le date ufficiali e quelle astronomiche). Su suggerimento del matematico alessandrino Sosigene il pontefice massimo Giulio Cesare nell’anno 708 di Roma (46 a.C) operò la riforma del calendario: in quell’anno (detto anno della confusione) furono inseriti oltre al mercedonio di 23 giorni altri due mesi (tra novembre e dicembre); fu considerato l’anno tropico di 365,25 giorni e pertanto, dopo tre anni di 365 giorni, veniva considerato un anno di 366 giorni.

Il giorno in più fo inserito tra il 23 e il 24 febbraio e fo chiamato bis sexto Kalendas Martias perché ripeteva il sesto giorno precedente le calende di Marzo, donde il nome di anno bisestile dato all’anno di 366 giorni. Il calendario giuliano è tuttora seguito dalla Chiesa cristiana russo-ortodossa. La reale durata dell’anno tropico è di 365,2422 mentre il calendario giuliano considerava 365,25. La differenza è 0,0078 giorni, poco meno di 0,01 (un centesimo di giorno); differenza insignificante per qualche secolo, ma che finì per diventare sensibile dopo molti secoli. Così, mentre all’epoca del Concilio di Nicea (325 d. C.) l’inizio della primavera cadeva il 21 marzo (ai tempi di Cesare si riteneva cadesse fra il 25 e il 26 marzo) nel 1582, cioè dopo 1257 anni, cadde l’11 marzo. Non a caso Dante nel 1300 scriveva nel Paradiso XXVII 142/143… prima che gennaio tutto si sverni / per la centesma ch’è laggiù negletta… facendo presente l’opportunità della riforma del calendario.

Nel 1582 papa Gregorio XIII, secondo un piano elaborato da Luigi Giglio (Lilius), medico e astronomo calabrese, promulgò la nuova riforma del calendario, ordinando che si sopprimessero intanto 10 giorni, passando dal 4 ottobre 1582 al 15 ottobre e stabilendo i giorni bisestili secondo la riforma giuliana (gli anni divisibili per quattro) escludendo gli anni secolari (che sono anni comuni, non bisestili) ma riconsiderando bisestili gli anni secolari quadricentenari. L’anno tropico del calendario gregoriano è considerato di 365,2425, con un errore di un giorno ogni 33 secoli circa. Questa lettura, in gran parte, è stata tratta dal libro del prof. Giuseppe Severino di Astronomia nautica (edizione CEDAM).

La meridiana.

Una meridiana è formata da un piano verticale orientato per Est-Ovest, da uno stilo o gnomone e da linee orarie: si veda la figura del retro copertina del libro. Le linee orarie, di colore rosso, hanno origine dal centro del particolare goniometro da cui si erge lo stilo che è nel piano meridiano, inclinato verso il basso dell’angolo (90° < φ) rispetto al piano verticale (φ: latitudine del luogo). Con tale inclinazione lo gnomone è parallelo all’ asse polare terrestre. Lo stilo è individuabile dal colore rosso della sua estremità.

Tra le linee orarie fondamentale è quella centrale, verticale: la meridiana che raccoglie l’ombra dello stilo nell’ istante il cui il sole transita, alle nostre latitudini, al meridiano superiore del luogo verso Sud (v. figura in alto). Le due figure in basso sono il retro della stessa tavola verticale; vi si nota lo gnomone inclinato verso l’alto dell’angolo (90 < φ) rispetto al piano verticale, sempre nel piano meridiano; questa faccia della tavola è rivolta verso Nord e raccoglie i raggi solari dal giorno dell’equinozio di primavera (20 o 21 Marzo) fino all’equinozio di autunno (23 o 22 settembre), dal sorgere e durante le prime ore del mattino ed in quelle del pomeriggio avanzato fino al tramonto.

La lettura dell’ora si fa dopo aver individuato l’ombra dello gnomone, generalmente interpolando tra due linee orarie. Osservando la figura in alto: ora solare tv” = 10 h 55 m ; l’ora antecedente (del mattino) è tv’ (figura in basso a sinistra) 6 h 50 m ; l’ora pomeridiana (P.M.) tv”=4 h 49 m , cioè pari a 16 h 49 m , letta sulla figura in basso a destra. L’approssimazione nelle letture è stimabile in 4 o 5 minuti. Le letture sono del giorno 21 Giugno, solstizio estivo. Le corrispondenti ore legali, o del fuso, sono: ora legale = tv + ε + (λ f – λ) + 1 h ; ora del fuso = tv + ε + (λ f – λ); primavera – estate autunno – inverno , equazione del tempo, si legge nella tabella (v. oltre) in funzione della data, interpolando. (λf – λ) è la correzione del fuso: distanza del meridiano del luogo, di data longitudine λ, dal meridiano centrale del fuso λf (l h ,2 h , 3 h … fino a 12, + se Est, – se Ovest).

La meridiana della figura è stata costruita nel punto φ = 39°11′ N, λ= 8° 15′ E circa; il valore di λ in ore e minuti è 0 h 33 m . Pertanto: (λ f – λ) = (1 h – 33 m ) = 27 m . Ricordiamo che 1° = 4 minuti; 15′ = 1 minuto e che la località si trova nel fuso 1 h E. La  tratta dalla tabella, per il 21/6, è + 2 m . Corrispondenti ore legali, ordinate nel tempo: 8 h 19 m 12 h 24 m 18 h 18 m Costruzione delle linee orarie. Ricordiamo che 1 h = 15°. Le coppie di linee orarie simmetriche (v. fig. in alto) sono: XI-I; X-II; IX-III; e così via. Esse sono lontane, angolarmente, dalla linea meridiana centrale, dell’ angolo α determinabile con la formula: tan α = cos φ ∙ tanP; P = 15°(1 ) per la prima coppia; 30°(2 ) la seconda coppia; 45°(3 ) per la terza …

Esempio numerico: per φ = 39°11′ gli angoli risultano: 11,7° 24,1° 37,8° 53,3° 70.9° 90°. Per le figure sottostanti prosegue la successione dei valori: 109,1° (coppia V A.M. e VII P.M.); 126,7° (coppia IV A.M. e VIII P.M.).

Nota. Lo studente che conosce la sfera celeste sa ricavare la relazione di α considerando il triangolo sferico rettangolo avente i vertici: Pcn, Z (zenit in cui l’angolo è 90°), V (punto d’intersezione dell’orario P con il l° verticale Est-Ovest). Lunghezza dell’ombra e le stagioni.

Il lettore avrà notato, nelle tre figure, la presenza di tre “soli”: giallo per indicare “quello” del solstizio estivo (2116), “verde” per “quello” del solstizio invernale (22/XII), “giallo-verde” per gli equinozi (2113 e 23/9). Sulla meridiana rivolta a Sud, con gli stessi colori sono state tratteggiate le curve descritte, nelle ore, dalle estremità delle ombre dello stilo nei quattro giorni principali sopra ricordati. In particolare: due coniche nei due giorni solstiziali e una retta nei due giorni equinoziali.

Un’approssimativa interpolazione sull’ombra, nei giorni intermedi, consente di risalire al mese. Nella figura in alto è evidente il giorno 21/6. Per una data lunghezza l dello stilo, la lunghezza dell’ombra a mezzodì (XII, istante del transito del sole al meridiano), è data da: l∙sen α + l∙cos α / tan(φ - δ). Esempio: per l =16 cm, le tre lunghezze, per le tre epoche, sono: 54,1 cm (21/6), 25,3 cm (equinozi), 16,5 cm (22/12). I due termini della relazione danno le lunghezze dei cateti dei due triangoli rettangoli in cui viene scomposto il triangolo CEO (C pedice dello gnomone, E apice, O estremità dell’ombra) abbassando da E la normale al piano della tavola. Non ci dilunghiamo con altre formule più complesse perché le imperfezioni strumentali (ne ricordiamo solamente due: l’imperfetta verticalità della tavola, comunque controllabile col filo a piombo; l’imprecisa orizzontalità della base – rosa dei venti – verificabile con la livella a bolla) sono tali per cui è consigliabile controllare che i risultati dei calcoli siano vicini alle risultanze empiriche.

Rosa dei venti.

È la superficie di appoggio, tramite scassa, della meridiana. Ricordiamo come s’individua la linea Sud-Nord. Si mette un’asta perfettamente verticale e si insegue, segnandola, l’ombra più corta. Ci deve essere una pratica coincidenza: l’ombra più corta si ha all’ora legale o del fuso: ora legale = 12 h + ε + (λ f – λ) + 1 h ; ora fuso = 12 h + ε + (λ f – λ). L’epoca più favorevole è uno dei giorni prossimi al solstizio, invernale o estivo. Sulla rosa sono visibili i soli giallo e verde nelle direzioni in cui sorgono e tramontano; la distanza angolare da Est e da Ovest è l’Amplitudine (Ampitudine calcolabile con la formula senAmpl = sen 23°26’30″ / cos φ).

Gli stessi soli compaiono sulle due superfici della meridiana ed indicano le ore del sorgere e del tramonto; ore calcolabili con la formula cosP = -tan φ ∙ tan 23°26’30″. Negli equinozi (“sole” giallo- verde) il sole sorge a Est e tramonta a Ovest, 6 ore prima e 6 ore dopo l’ora del transito al meridiano. Per ogni epoca si prescinde dalle dimensioni del sole, ritenuto puntiforrne, dalla rifrazione astronomica, dalla elevazione dello strumento rispetto alla quota zero. Sullo sfondo blu della rosa dei venti sono state disegnate due costellazioni fondamentali per l’orientamento: la Croce del Sud (circumpolare invisibile alle nostre latitudini), non lontana dal polo celeste sud, e l’Orsa Maggiore.

Il prolungamento, per 5 volte, della distanza delle ultime due stelle del “Carro”, Merak e Dubhe, individua la stella Polare, vicinissima al polo celeste nord. Dall’orientamento di tale prolungamento rispetto alla congiungente Polare-Zenit dell’osservatore si può risalire all’individuazione dell’ora in qualsiasi istante della notte, in φ nord, grazie al moto apparente delle stelle.

ε equazione del tempo (nei giorni 6 e 21 di ogni mese, circa)

Nei discorsi della meridiana e della rosa dei venti sono racchiusi molti concetti di cosmografia: ecco un’esercitazione efficace; aiutare gli allievi di buona volontà a costruire l’orologio solare, un po’per volta, dal solstizio invernale a quello estivo. Diceva un poeta arabo che l’uomo occidentale ha cominciato a perdere il contatto con la natura da quando, affrettando il suo passo, si è allontanato dal ritmo lento dello scorrere delle ore e del graduale cambiamento delle stagioni, dalla visione delle stelle e dall’osservazione del mutamento ciclico delle costellazioni del firmamento, con astri che vanno al tramonto eliaco e dopo uno o due mesi riappaiono, declinano, si riavvicinano al sole: mistero e poesia del Creato.

Lettura. Regolazione degli orologi di bordo sul tempo vero t v durante la compensazione o il controllo della bussola magnetica.

Ricordiamo le relazioni tra i tempi:

t m = t v + ε ;

t f = t m + (λ f – λ ) ;

t v = t f – (λ f – λ ) – ε

Esempio: Il giorno 1 Maggio la nave è in φ 24°06’ Nord λ 21° 30’ W; declinazione magnetica d: = 12°36’ W.

Al mattino del giorno 1 / V viene effettuato un giro di bussola per il ritocco della compensazione. Nei preliminari c’è lo spostamento di uno dei due orologi da polso, dal tempo fuso t f al simultaneo corrispondente tempo vero t v . La correzione del fuso risulta : (λ f – λ ) = -15° – ( – 21°,5) = + 26 minuti; l’equazione del tempo, tratta dalle Effemeridi,: ε = – 3 minuti. La correzione complessiva è + 23 minuti. Verso le ore t f 8 h 30 m , un orologio regolato sul fuso subisce lo spostamento delle lancette per leggervi l’ora solare vera t v (spostamento indietro di 23 minuti); l’orologio segna: t v = 8 h 07 m . Il compensatore lavorerà con questo orologio del tempo vero.

Il compensatore, che conosce le Tavole , sa che alle 8 h 32 m (VIII 32 m ) è riportato l’azimut vero del Sole (uno fra tanti, intervallati di 4 minuti). Predispone il traguardo azimutale sulla bussola di controplancia e misura il primo rilevamento del “giro di bussola” appena il suo “orologio vero” (t v ) segna 8 h 32 m : azimut bussola a b = 100°. Legge sulle Effemeridi la declinazione del Sole: δ 15°N (con lieve arrotondamento); apre le Davis sulla pagina intestata alla latitudine φ 24° omonima della declinazione 15° N del Sole. Legge sulle tavole Davis, in corrispondenza dell’ora VIII 32 minuti, il seguente azimut: a v = 90°,4 sulla Prora bussola Pb 000.° Calcolo della variazione V (d + δ ev. ) e della deviazione δ ev.

V = a v – a b ;

V = 90°,4 – 100° ;

d = 12°,6W

δ = V – d ;

δ = – 9°,6 +12°,6 ;

V = – 9°,6 δ = + 3°,0 ;

I Nota. L’argomento sulla compensazione di bussola è riportato sul trattato Navigazione tradizionale, e in misura esaustiva nel sito di Quaderni Marinari.

II Nota. Nei primi anni 80 arrivò a Genova una nave inglese proveniente dal Sud Africa. Aveva nelle stive ferraccio. Durante il viaggio andò fuori uso l’unica girobussola. Inoltre il campo magnetico creato dal ferraccio alterò notevolmente la compensazione. Gli Ufficiali, durante le guardie diurne e notturne dovettero controllare ripetutamente la deviazione della magnetica. Lo fecero sia di giorno, col Sole, sia di notte con le stelle: orologi regolati sul tempo vero e sul tempo sidereo.

Lettura: Regolazione degli orologi sul tempo medio t m

Parliamo di una regolazione che viene considerata solamente nelle lunghe traversate oceaniche. Gli orologi alla partenza viaggiano sul t f .

Ricordiamo la relazione algebrica:

t m = t f – (λ f – λ) m

dove il termine tra parentesi è la correzione del fuso.

Sia A il punto di coordinate (φ A , λ A ), punto iniziale della traversata per raggiungere B (φ B , λ B ). La lancetta dei minuti è da spostare indietro se dal calcolo risulta t m < t f , in avanti se t m > t f .

Tale calcolo del t m è la prima fase, orientativa, riguardante la regolazione degli orologi sul tempo medio. Poi si passa a considerare la correzione complessiva

Ccg = [- (λ f - λ A ) m + (λ B - λ A ) m ] / N

Nell’espressione di “Ccg”, N è il numero dei giorni previsti di navigazione, tenendo conto della velocità della nave: Ccg è considerata costante. I segni delle due correzioni parziali: (λ B – λ A ) m , prevalente, è positiva quando la rotta complessiva della traversata è verso levante; negativa se è verso ponente. – (λ f – λ A ) m ha il segno contrario della correzione del fuso, da cui parte la nave. Poiché la correzione (λ B – λ A ) m è prevalente, si può concludere:

- lancette in avanti se si va verso oriente;

- lancette indietro se la si naviga verso occidente.

Questa variazione, praticamente, viene calcolata dall’allievo (con l’avallo del Primo Ufficiale) e comunicata alla Macchina, ogni giorno, durante la “guardia diana” dalle 4 alle 8 antimeridiane. Nella pratica di bordo tale ora è indicata con t b , tempo di bordo. È cura dell’allievo muovere le lancette degli orologi nelle sale di mensa.

In prossimità dell’arrivo si riportano gli orologi sul t f del punto di destinazione B. Si opera il confronto tra l’ora di bordo t b ed il simultaneo t f ; (t f = T m + λ f di B), dove T m = Tc + K.

Questo metodo, apparentemente un po’ complicato nelle parole, ma non nell’operatività (come trasparirà dallo svolgimento di un esempio numerico), ha un vantaggio non trascurabile per la salute del marittimo.

La distanza media Terra-Sole è 149.504.000 km, l’unità astronomica (U.A.), è 149.600.000 Km. raggio effettivo 696.000 Km.; semidiametro apparente (σ) 16′ (valore medio). Massa 1,99 x 10 30 Kg. (oltre 330.000 volte maggiore della massa terrestre); densità media (ρ) = 1,41 g/cm 3 ; gravità: 27,9 g (g è la gravità terrestre: 9,81m/sec 2 ).

Temperatura sulla superficie (fotosfera): 65000°C; temperatura verso il nucleo: circa 10 milioni di gradi; pressione al centro: circa 10 miliardi di atmosfere. Età del Sole: 4,6 miliardi di anni, sono stimati 5 miliardi di anni di vita futura. Nel Sole sono stati accertati, con l’analisi spettroscopica oltre 60 elementi. Prevalgono, con 1’80%, gli atomi di idrogeno e poi, in ordine decrescente, elio, ossigeno, carbonio, azoto, silicio, magnesio…

Il Sole irradia continuamente circa 90.000 calorie per cm 2 al minuto. Qual è l’origine di un’energia così immensa? La risposta è: la trasformazione dei nuclei atomici. Da quei valori enormi di densità (al centro), di pressione, di temperatura è facile immaginare una elevata velocità di diversi atomi che, dal loro scontro, si trasformano dando origine alle cosiddette reazioni termonucleari di fusione. Nel sole quattro nuclei d’idrogeno H si trasformano in nucleo di elio (He): reazione di trasformazione 4H 1 4032 → 1He 4 4003 ; 1008 (4032:4) e 4003 sono i pesi atomici dell’idrogeno e dell’elio.

La massa m che scompare, dalla reazione, 0029 cioè 29, si trasforma in energia E. E = mc 2 dove c = 300.000 Km/s circa è la velocità della luce. Lo strato solare esterno alla fotosfera è la cromosfera, visibile durante un’eclisse totale di sole. In esso avvengono lanci di materia, gas incandescenti, chiamati protuberanze o brillamenti o «flares» alte centinaia e talvolta migliaia di Km. Esternamente alla cromosfera c’è la corona, costituita prevalentemente di raggi X. Le macchie più grandi superano la dimensione della Terra, tanto da essere visibili ad occhio nudo. Le macchie «si muovono» e denunciano chiaramente una componente di moto da un bordo all’altro del Sole, indice certo della rotazione differenziale del Sole in circa 27 giorni. La velocità aumenta dall’equatore solare verso i poli. Il sole è sede di un campo magnetico.

Si pensa che le macchie solari siano l’effetto di caduta di gas fortemente ionizzati provenienti da piccole protuberanze. L’atmosfera di idrogeno, circondante le macchie, sarebbe costretta a muoversi, sotto l’influenza di questi intensi campi magnetici, in un vortice gigantesco. Il ciclo di questa attività è 11 anni circa. La radiazione emessa dal sole abbraccia tutte le frequenze, e quindi le corrispondenti lunghezze d’onda, comprese fra le radioonde metriche e i raggi γ. Le più numerose sono comprese fra 0,17 μ e 8 μ (1 micron μ = 10 -3 mm.); la banda visibile è compresa fra 0,4 e 0,8 μ (violetto-rosso).

I raggi X del Sole ionizzano, tra i 45 e 300 Km, la nostra atmosfera creando le fasce di ionizzazione. Tra tutte le particelle prodotte nelle varie reazioni termonucleari interne solo una, il neutrino, raggiunge la superficie solare. I neutrini hanno massa nulla e viaggiano alla velocità della luce. Provenendo dall’interno del Sole hanno un notevole interesse astro fisico. Una trappola gigantesca per neutrini è stata collocata in caverne del Gran Sasso e del Sud- Dakota, molto al di sotto della superficie terrestre. Il sole emette energia anche sotto forma «corpuscolare» o «plasma» che in occasione dei brillamenti aumenta notevolmente d’intensità; essa costituisce il cosiddetto vento solare comprendente ioni ed elettroni. La velocità è circa 350-400 Km/sec. Le fasce di Van Allen, a 3600 e a 16000 Km, avvolgono, salvo i poli, tutta la Terra.

Sono costituite da neutroni e protoni primari, ad alta energia, provenienti dallo spazio interplanetario, ma soprattutto dal vento solare e sono catturati dal campo geomagnetico. Le cinture di Van Allen contengono anche elettroni secondari dovuti alla ionizzazione degli atomi di quell’atmosfera rarefatta. Nei momenti di maggiore attività delle macchie solari si verifica, in corrispondenza di un aumento del vento solare, un aumento della ionizzazione degli alti strati dell’atmosfera terrestre, con conseguente aumento dell’assorbimento delle radioonde da parte della ionosfera, interferenze e disturbi vari (tempesta magnetica). In corrispondenza delle tempeste magnetiche più intense si verificano, alle alte latitudini, stupende luminescenze degli strati superiori dell’atmosfera terrestre: aurore boreali o polari, conseguenti ad un abbassamento delle fasce di Van Allen.

L’uomo, fin dalla preistoria ha cercato di dare un ordine alle attività lavorative giornaliere, mensili e annuali.

Il rispetto dei tempi: della semina e della raccolta, dei lavori sui campi, le temporanee migrazioni, vicine o lontane; tutto ciò in armonia con l’alternarsi del giorno e della notte e con il ciclo delle stagioni.

Il «tempo» andava suddiviso e tale suddivisione doveva essere nota ai membri di una stessa comunità. Il corso diurno del Sole ha tre istanti: sorgere, transito alla massima altezza, tramonto, che dividono già la giornata in ore antimeridiane ed in ore pomeridiane. Un’ asta –lo gnomone – piantata verticalmente su un pianoro orizzontale, era utile allo scopo: l’ombra più corta divideva le ore antimeridiane da quelle pomeridiane. La suddivisione in ore non fu immediata. Quando si pensò di mettere lo gnomone su un’elevata superficie verticale, visibile anche a distanza, si fece un passo importante per arrivare, con gradualità, ad una meridiana. Uscendo dalla preistoria l’uomo pensò alla organizzazione del lavoro, importante per la sopravvivenza. Le ore della notte? Poteva dare qualche riferimento il corso notturno della Luna.

Così fu; lo testimoniano i calendari lunari, antecedenti a quelli solari. Finché qualcuno pensò che la suddivisione della notte in ore era altrettanto importante. Un contenitore di argilla o terracotta, con un piccolo foro in basso fu la prima clessidra ad acqua. Il livello dell’acqua che scendeva gradualmente ed uniformemente (o quasi) è stato il primo misuratore del tempo o, per meglio dire, degli intervalli di tempo. L’osservazione del cielo ed i fenomeni celesti casuali, quali le eclissi, in particolare quelle di Sole, furono seguiti con interesse, ma anche con apprensione e talvolta panico (chi ha assistito ad un eclisse totale di Sole – col il passaggio quasi repentino dalla luminosità ad una luce simile a quella di un crepuscolo avanzato; al calo quasi repentino della temperatura – può comprendere meglio. I primi astronomi cominciarono ad annotare i fenomeni, a registrare le primavere entranti (col ritorno del Sole sorgente esattamente ad Est)…

Le annotazioni sistematiche erano appannaggio delle persone più curiose e che si ponevano delle domande sul mutevole alternarsi dei giorni e delle notti, delle stagioni e degli anni. Furono eretti osservatori in punti più elevati per avere il più ampio cerchio di visibilità. Questi primi astronomi sovente erano anche sacerdoti. La campana era sistemata nel punto più elevato del campanile; per essere udibile da molti, all’occorrenza, per segnalare con anticipo un incombente pericolo o, più semplicemente, dare modo a tutti di vedere la meridiana, di sentire i rintocchi della campana che segnala il mezzogiorno… I sacerdoti osservatori divennero così i depositari e custodi del tempo. Le clessidre ad acqua lasciarono il posto alle clessidre con sabbia, più pratiche e più precise. Confrontando le indicazioni della clessidra con quelle dello stilo della primitiva meridiana, qualcuno, provando e riprovando, intuì che l’angolo (tra lo gnomone inclinato verso il basso e la parete verticale) idoneo dovesse essere uguale a 90° – φ, (cioè, diciamo oggi, 90° – l’angolo di latitudine φ, angolo tra il piano orizzontale e la stella del Polo Nord). Dalle parti del Polo nord un tempo c’era Etamin (la stella polare fenicia denominata anche Thuban) stella della costellazione del Drago.

L’astronomo aspettò che sopraggiungesse il prossimo equinozio. Divise in sei parti uguali tutta la sabbia che scorreva dal sorgere del Sole fino al suo passaggio al meridiano (con la collaborazione dell’ombra più corta, sul piano orizzontale, di uno stilo verticale). Negli istanti in cui finiva di scorrere un sesto della sabbia, l’ombra veniva marcata sulla parete verticale del templi, luoghi di osservazione e di culto, sinagoghe o minareti. Di notte? Di notte ci sono i “notturnali”, i grandi orologi siderali dell’emisfero Nord e dell’emisfero Sud (si legga §1, Cap. XV ). Nel Medioevo il connubio tra la scienza astronomica e la religione nei monasteri, in parte si trasformò. A fianco al convento o venne mantenuto l’osservatorio astronomico o trovarono posto le biblioteche, dove i monaci ricopiavano i trattati letterari e scientifici più antichi, pertanto soggetti al deterioramento (se le aule non erano adibite ai lavori di manifattura). In ogni caso i monaci rimasero i «custodi del tempo».

Tuttora le loro funzioni e i loro lavori, sono cadenzati dalle preghiere e lodi…al rintocco della campana annunziante l’ora terza, sesta, nona… A proposito del suono della campana del mezzodì che dal campanile della chiesa si propaga ancora nella valle, il suono giunge gradito ai valligiani; ma – particolare curioso – non ai cani di razza, che ululano al pericolo… suggerito (a detta degli etologi) dalla loro forte memoria genetica, anche se è trascorso tanto tempo. Nota. A chi intendesse costruire una meridiana, il suggerimento è immediato: faccia marciare un orologio da polso sul tempo medio t m (v. Cap. VI); t m = tempo del fuso – correzione del fuso.

Il resto va da sé, seguendo il filo del discorso. Si può partire dall’ombra più corta del mezzogiorno e procedere. Le linee orarie, orientali ed occidentali, sono simmetriche rispetto alla linea meridiana. Una volta letta l’ora media solare t m , l’ora del fuso è:

t f = t m + correzione del fuso (λ f – λ )

Per una maggiore precisione: si costruisce la meridiana nei giorno in cui l’equazione del tempo (v. Cap. VI) è zero o quasi zero. All’ora letta si sottrae algebricamente l’equazione del tempo e si ottiene t m . Dal t m si tassa al t f .

Si propone la costruzione di un grafico con i valori numerici che seguono: sono relativi all’anno 2012; un evento astronomico che destò molto interesse: l’“avvicinamento“ di Venere-Giove alla distanza di circa 1°: si trattò ovviamente di un avvicinamento dal punto di vista della prospettiva. il passaggio avvenne tra Hamal (α Arietis) e Menkar (α Ceti) le cui coordinate sono nelle pagine delle Effemeridi.

Traiettorie di Venere in rosso e di Giove in blu

Le comete sono corpi celesti che rivoluzionano intorno al Sole descrivendo, generalmente, orbite ellittiche con grandissima eccentricità e rilevante inclinazione rispetto al piano d’eclittica. Una cometa essenzialmente formata da un nucleo, di 10-15 Km di diametro, costituito di materiale congelato, principalmente acqua e biossido di carbonio , misto a polveri.

La massa è modesta, in generale non supera il miliardesimo della massa della Terra. Quando la cometa si trova lontana dal sole il nucleo è inattivo, ma quando la cometa si avvicina al sole il calore fa evaporare parte del materiale congelato dando luogo alla chioma, che circonda il nucleo, e alla caratteristica coda. La coda si forma per l’effetto del vento solare sui gas di evaporazione che vengono sospinti lontano per centinaia di milioni di chilometri.

La coda, sempre opposta al sole, segue il nucleo nella fase di avvicinamento al perielio; lo precede nella fase di allontanamento; poi via via scompare. Durante la formazione della coda, specialmente intorno al perielio, la massa della cometa è soggetta ad una lieve e continua perdita.

Vi sono due tipi di comete: quelle che hanno orbite ellittiche e che quindi ritornano periodicamente (la cometa di periodo più breve, 3,3 anni è denominata Encke, quella di più lungo periodo noto, 76 anni, è Halley, con l’afelio entro l’orbita di Plutone) e quelle aperiodiche che hanno orbite iperboliche o paraboliche che, non essendo chiuse, passano una sola volta vicino al Sole e poi si disperdono nello spazio. La velocità è minima all’afelio e quindi le comete di lunghissimo periodo passano la maggior parte del tempo a distanze molto grandi dal Sole, formando una nube, detta nube cometaria di Oort (Jan Oort è l’autore di questa teoria) che si trova ad una distanza dal sole di oltre un anno luce. Porzioni della nube verrebbero dirottate, per qualche perturbazione esterna, verso il sole. Si pensa che le comete si siano formate 4,6 miliardi di anni fa. Il loro interesse scientifico sta proprio nel fatto che la materia di cui sono composte è molto antica e risale agli albori del sistema solare.

Da quando gli astronomi tengono traccia delle loro osservazioni, cioè in epoche storiche, sono state osservate più di 1000 comete. Dopo Tycho Brahe un grande studioso di comete fu E. Halley da cui prese il nome la cometa da lui lungamente studiata. Fu avvistata la prima volta, con certezza, dai Cinesi nel 240 a. C. ed è possibile che sia la vera cometa di Natale (anche se il dubbio in questo caso è dovuto all’anno esatto della nascita di Cristo e non alle conoscenze astronomiche). Halley predisse il ritorno nel 1758 ma non poté osservarla, morì qualche anno prima. È ritornata sui nostri cieli nel febbraio 1986. Fu inviata la sonda spaziale « Ciotto » per studiarne le caratteristiche fisiche; la sonda sfiorò il nucleo, fu danneggiata dall’urto di particelle cometarie, successivamente fu posta in orbita intorno al Sole.

A motivo della costituzione per così dire granulare del nucleo cometario l’attrazione gravitazionale del sole sui singoli materiali che lo compongono dà luogo ad una lenta disgregazione del nucleo stesso. Ciò avvenne per le comete di Tuttle, Tempel e di Biela e di altre ancora. La cometa Biela fu scoperta da Schiaparelli nel 1826. La cometa riapparve nel 1846 con due nuclei. Il 27 novembre 1872 invece delle due comete venne notata una pioggia intensissima di stelle cadenti, oltre 30. 000 in sei ore: la Terra in quel giorno tagliava l’orbita della scomparsa cometa Biela! Le meteore, incontrando l’atmosfera terrestre e attraversandola a grandissima velocità s’incendiano per l’elevato attrito; i frammenti più grossi, meteoriti o bolidi, talvolta si schiantano sulla superficie terrestre. Tra i tanti meteoriti si ricorda la « pietra nera» della Mecca, tanto adorata dai maomettani.

L’astronomo C. Schiaparelli (1835-1913) fu un grande studioso di comete.

Le stelle cadenti sono più numerose nella prima decade di agosto e in novembre. Sembrano provenire da un certo punto del cielo denominato radiante. Il radiante di agosto è nella direzione della costellazione del Perseo; in novembre i radianti sono nelle direzioni delle costellazioni del Leone e dell’Andromeda. Non tutte le stelle cadenti hanno origine dai residui cometari; sporadici aereo liti provengono dagli spazi siderali occupati dalla nube di Oort o da nebulose oscure (1).

Infine nel cosmo del sistema solare c’è la polvere meteorica, minutissimi « sassolini» che hanno lasciato abrasioni nei veicoli spaziali.

I fenomeni delle comete e dei meteoriti, affascinanti quanto ancora misteriosi, hanno suggerito a G. Pascoli i bellissimi versi della poesia X Agosto; ne ricordiamo alcuni: « S. Lorenzo … / E tu, Cielo, dall’alto dei mondi / sereni, infinito, immortale, / oh, d’un pianto di stelle lo inondi / questo atomo opaco del Male ». 

(1) Presso la stella γ Andromedae c’è la famosa nebulosa di Andromeda (M 31) galassia del tutto simile alla nostra Via Lattea, unica galassia esterna visibile a occhio nudo e la più vicina (700 mila anni luce) dopo le Nubi di Magellano che sono considerate piuttosto galassie satelliti del nostro sistema. La composizione stellare della Galassia fo inconfutabilmente dimostrata da Herschel e da Galileo.

Le posizioni reciproche Terra, Sole e costellazioni danno luogo a fenomeni celesti interessanti ma di non immediata interpretazione. Pertanto è opportuno assecondare la lettura delle note che seguono seguendo la figura simile a quella del paragrafo Tramonto e sorgere di Sirio; ma completamente in chiave reale. Tutto ciò per meglio capire le fasi di opposizione, tramonto eliaco, congiunzione, sorgere eliaco, e ritorno all’opposizione.

“Una sera un viandante nota una costellazione -elevata non più di 25° rispetto all’orizzonte- mai notata prima, ma che dalla forma intuisce che debba essere la costellazione dello Scorpione (per i tre tentacoli e la coda in basso). È il 30 Maggio. Dirige verso il lungomare per osservarla davanti alla rosa dei venti: qualche grado meno di 180°. Si allontana e si propone di ritornare.

Osserva di nuovo Antares: ora è proprio a Sud; a mezzanotte, 24.00 del 30 Maggio. Ha un primo significativo dato: la stella più luminosa –Antares α Scorpii– stava transitando al meridiano; indicazione data dal rilevamento 180°, Sud. Antares è in opposizione al Sole a mezzanotte del 30 Maggio.

Iniziò da quella sera una sistematica attenzione al cielo stellato in generale, ma in particolare per la suddetta costellazione per capire, possibilmente, qualcosa di più sulla combinazione dei moti diurno e annuo del nostro pianeta e per cominciare a conoscere le costellazioni.

L’osservatore è in latitudine 40° Nord, circa. Il lettore può seguire meglio il discorso dando contemporaneamente uno sguardo alla cartina del cielo stellato.

La sera del giorno dopo la serenità del cielo gli consente di rivedere Antares e la sua corte di stelle (la seconda stella molto luminosa è λ Scorpii: Shaula) appena sopra l’orizzonte, per E-SE circa. Un suggerimento al lettore è quello di disegnare una figura simile a quella di Sirio. Costellazione dello Scorpione, orbita di rivoluzione della Terra intorno al Sole; il piano orizzontale dell’osservatore è disegnato con un segmento tangente; tale piano orizzontale è riportato all’esterno della sfera celeste; piano visto dall’osservatore che dà le spalle al cardine Nord. I quattro punti significativi sono corrispondenti a: Congiunzione (1 Dicembre), preceduta dal tramonto eliaco il 26 Ottobre, seguita dal sorgere eliaco il 27 Dicembre; Opposizione (30 Maggio).

Si fa notare che il piano orizzontale dell’osservatore ruota continuamente, per effetto della rotazione terrestre:

Inoltre la sua rotazione da 1 – 1 a 2 – 2 sia al sorgere che al tramonto è antioraria, come la rotazione della Terra.

I semipiani orientali (E) ed occidentali (W) dell’orizzonte sono “visti” da un osservatore che dà le spalle al Nord.

Scorpione era appena sorta, alle ore 20 e qualche minuto. Alla prima alba del giorno dopo l’astrofilo scorge la costellazione; la vede vicina all’orizzonte e declinare verso il suo tramonto: avvenuto alle ore 4 circa.

Era scattata nel viandante la molla della curiosità per l’Astronomia. A distanza di un mese, il 29 Giugno l’astrofilo ritorna sulla rosa dei venti per annotare l’ora del transito di Antares al meridiano (Sud): ore 22.00.

Riflette: due ore di anticipo accumulato in 30 giorni. 120 minuti in 30 giorni. 4 minuti al giorno .. Ecco: “l’apparente anticipo, detto accelerazione delle stelle fisse”! (o ritardo del Sole, come anche può essere denominato!); comunque una questione di calendario; riflette qualche secondo e conclude: “sì! sarà quasi certamente (ma senza quasi!) è il movimento apparente del Sole intorno alla Terra in senso antiorario!

È il reale senso di rivoluziona della Terra intorno al Sole. “Farò qualche calcolo di verifica con le Effemeridi”.Antares e l’astrofilo 2

La notte del 29 Giugno, alle ore 24, la costellazione è proprio all’opposizione rispetto al Sole: Sole – Terra – Scorpione, sullo sfondo del firmamento. Dalla mezzanotte di quella prima sera (30 Maggio) era iniziato il moto apparente di avvicinamento di Antares verso il Sole.

Disegna la figura col moto di rivoluzione della Terra (sempre ruotante intorno al proprio asse polare). Mette il punto della futura congiunzione C del Sole con Antares (metà anno, sei mesi circa, dalla opposizione O). In congiunzione –C– col Sole, Antares non sarà visibile. Si ricorda di aver letto che prima della fase di congiunzione c’è un giorno in cui Antares sarà visibile, l’ultima volta prima di entrare nella fase di offuscamento nella luce solare: il cosiddetto “tramonto eliaco” dopo il tramonto del Sole. “Farò dei calcoli in merito”. Li farò anche per conoscere la data del sorgere eliaco, al primo mattino, prima del sorgere del sole: “sorgere eliaco”. Considera che i due punti, tramonto e sorgere eliaci, non sono simmetrici; per essere simmetrici con la congiunzione l’ascensione retta deve essere 90° o 270° (asse solstiziale di simmetria con l’eclittica). I risultati (già anticipati) sono: tramonto eliaco 26 Ottobre, sorgere eliaco: 27 Dicembre. Nel paragrafo precedente sono stati descritti questi eventi con l’enfasi dell’immaginazione di essere insieme alle antiche popolazioni dell’Egitto, e della Magna Grecia in generale.